Python Lists: A closer look, part 2

Note: The first post in this series discussed why Python lists are such clean data structures to work with. The next post covers list comprehensions.

I love using lists in Python because in simple use cases, they’re extremely easy to use. If you can create the list you need and work with it in the ways you need, and your program generates the correct output and has reasonable performance, then you don’t need to look beyond the basics of how lists can be used.

However, some use cases push lists beyond their limits. People have a tendency to criticize Python as being slow when they first encounter these limits. But often times, a better understanding of how Python manages the data in a list leads to straightforward solutions that keep our programs performant. In this post, we’ll look at one illustrative way that lists can slow down, why it happens, and what you can do about it.

Appending to an empty list

One common way to build a list is to start with an empty list, and then append individual items to it. This isn’t always the most efficient way to build a list, but sometimes it’s necessary. If it works well enough for your use case, then it doesn’t matter too much whether it’s the “best” way to define a list. I’m a big fan of clearly defining what kind of performance is good enough in any given situation, and once you meet that level of performance anything else is probably premature optimization.

Let’s simulate a sequence of dice rolls, where each roll is a number from 1 to 6. We’ll build the sequence by appending to an empty list, and see how many rolls we can make before the program slows down. Here’s the loop that creates the list:

# random_numbers.py

from random import randint

# Build a list of random numbers, to simulate rolling a die.
rolls = []
for _ in range(1000):
    roll = randint(1,6)
    rolls.append(roll)

If you haven’t seen the randint() function before, it returns a random integer between the two values you provide. Here the call randint(1, 6) returns a random number between 1 and 6, including each of the boundary values 1 and 6.

We start with an empty list called rolls, and then start a loop that will run 1,000 times. If you haven’t seen an underscore used as a variable before, it’s used in situations like this where the loop variable won’t actually be used inside the loop. On every pass through the loop, we generate a new value for roll and append that value to the list.

Let’s add a few more lines to examine the output, which will be useful as we push the limits of this approach:

# random_numbers.py

from random import randint

# Build a list of random numbers, to simulate rolling a die.
rolls = []
for _ in range(1000):
    roll = randint(1,6)
    rolls.append(roll)

# Verify how many rolls were generated.
print(f"Generated {len(rolls):,} rolls.")

# Print the first ten rolls, and the last ten rolls.
print(f"First ten rolls: {rolls[:10]}")
print(f"Last ten rolls: {rolls[-10:]}")

In an f-string, the modifier :, is a format specifier that tells Python to insert commas at appropriate places in a number. Here’s the output:

Generated 1,000 rolls.
First ten rolls: [2, 2, 1, 6, 2, 3, 6, 4, 1, 4]
Last ten rolls: [2, 2, 1, 5, 5, 5, 3, 5, 1, 2]

We can see that we made a list of 1,000 rolls, and the results look like what we’d expect to see.

Pushing append() to its limits

Now let’s increase the number of rolls, until this small program takes over 10 seconds to run. That number will depend on the system’s specs, but it will give an example of when a list might break down.

Using a simple approach to timing, this approach slows down significantly on my system at about 20 million rolls:

$ time python3 random_numbers.py
Generated 20,000,000 rolls.
python3 random_numbers_10s.py  13.22s user 0.16s system 96% cpu 13.847 total

This took just over 13 seconds, which is slow enough that we can compare it to other approaches.

Note: We’ll look at more accurate approaches to profiling later in this series. I’ve also simplified the output to show just the number of rolls that were generated.

Using insert() instead of append()

Using append() in this example means the first roll is the first item in the list, and the most recent roll is the last item in the list. What if you always wanted the most recent roll to be at the beginning of the list?

Here’s a loop that builds a similar list, but it always places the first roll at the start of the list:

# random_numbers_insert.py

from random import randint

# Build a list of random numbers, to simulate rolling a die.
#   The most recent roll is always first in the list.
rolls = []
for _ in range(100):
    roll = randint(1,6)
    rolls.insert(0, roll)

# Verify how many rolls were generated.
print(f"Generated {len(rolls):,} rolls.")

Here we’re using insert() instead of append().

Again, let’s find out how far we can push this approach. We’ll increase the number of rolls until it takes about 13 seconds to run this program. Instead of 20 million rolls, we only get 220,000 rolls:

$ time python3 random_numbers_insert.py
Generated 220,000 rolls.
python3 random_numbers_insert.py  13.56s user 0.10s system 91% cpu 14.896 total

The first approach lets us generate a list with about 100 times as many elements as this new approach! Why are these results so different?

How big is the shelf?

In the previous post I wrote that a shelf is a good metaphor for a list. Let’s be more specific about the kind of shelf Python sets up when you start to work with a list.

In languages like C, you have to declare exactly how many elements will go into a sequence. The language then reserves exactly enough space to store those items. In Python, we don’t specify how much space we need, so Python has to make a good guess. A visualization of the “shelf” that Python creates might look like this:

This shelf is empty, corresponding to an empty list. We can add some items, and we start to use up the space that was originally reserved for the list:

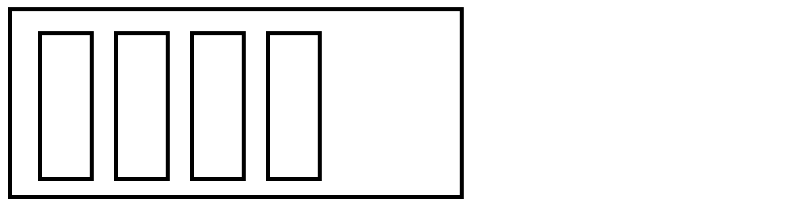
As we add items, Python recognizes that the list is running out of room. It grabs some more space, to make sure there’s always room for more items:

We keep adding items, mostly unaware that Python has grabbed more space:

This process repeats, as often as necessary to accommodate all of the items that are added to the list.

Is this efficient?

This process is relatively efficient. The algorithms for deciding how much space to reserve at any given time have been optimized over a period of decades now. With any collection, there’s a tradeoff between how much memory we’re consuming, how fast the operations happen, and how much we have to pay attention to memory management. For a large number of use cases, Python’s implementations just work.

What about insert()?

The algorithm for deciding how much space to allot for a list has been optimized for appending; most people add on to the end of a list.

Python doesn’t plan on people inserting items at the beginning of a list frequently. When you make a call like rolls.insert(0, roll), Python has to shift all of the existing items to the right one space, and then assign the new value to the first slot in the list. This is an expensive operation, and it gets more expensive as the list grows.

Using a deque

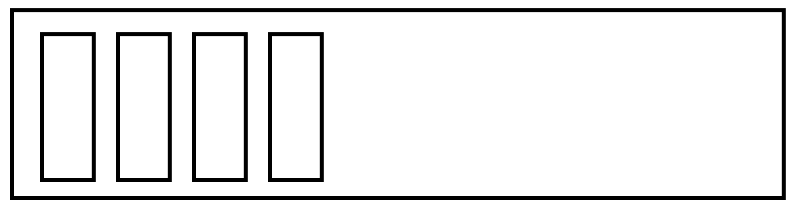
If you know you’ll need to insert items at the beginning of a sequence, you can use a slightly different data structure. The standard library contains a structure called a deque, a sequence that’s optimized for adding items at either end. The term deque is short for double-ended queue. When you create an empty deque, the empty shelf is still a good metaphor. However, when you start to add items, Python keeps some space at either end of the collection. Here’s a representation of a deque with four items in it:

The empty space on either side of the sequence means you can efficiently add items to the beginning or the end:

# random_numbers_deque.py

from random import randint
from collections import deque

# Build a list of random numbers, to simulate rolling a die.
#   The most recent roll is always first in the list.
rolls = deque()
for _ in range(20_000_000):
    roll = randint(1,6)
    rolls.appendleft(roll)

# Verify how many rolls were generated.
print(f"Generated {len(rolls):,} rolls.")

We import deque from the collections module, and initialize rolls to be an empty deque. Inside the loop, we use the appendleft() method. Since a deque is made for appending to both sides, it has both the append() method that you’re probably familiar with from working with lists, and its own appendleft() method. This method has the same effect as calling insert(0, roll).

This is about as efficient as appending to a standard list:

% time python3 random_numbers_deque.py
Generated 20,000,000 rolls.
python3 random_numbers_deque.py  13.13s user 0.14s system 99% cpu 13.343 total

We’re back to about 20 million items in just over 10 seconds.

When should you use a deque?

A deque is used whenever you need to do frequent operations at the beginning of a list. This article has focused on adding items to the beginning of a sequence, but repeatedly removing items from the beginning of a list would suffer a similar performance hit. When you call pop(0) on a list to remove the first item, all of the remaining items shift one position to the left. A deque is optimized for insertions and deletions from both ends of the sequence, and doesn’t suffer this same performance hit.

For example, if you need to implement first-in, first-out (FIFO) functionality, a deque will retain higher performance levels as your operations increase in speed and volume, where a list would slow down.

Be aware that a deque doesn’t have all of the same functionality as a list. For example a deque does not support slices; if you want a section of a deque you’ll need to use the islice() method from the itertools library.

You may never need a deque in your own work. But understanding why they exist helps you understand how lists and other sequences are implemented, and what kinds of things can be done to address the performance limitations of any given data structure.

Note: To pop an item from the beginning of a deque, use the special popleft() method. For more information, see the official documentation for deque, and for the collections module in general.

Lists in memory

It can help to visualize the size of a list as we add elements to it. The sys.getsizeof() method tells you the size of any Python object, in bytes:

>>> import sys
>>> sys.getsizeof("Hello")
54

The string "Hello" takes up 54 bytes in memory.

If we add elements to a list one at a time, we might expect the size of the list to increase as each item is added. Let’s write a short program to test this idea:

# list_memory.py

import sys
from random import randint

# Build a list of random numbers, to simulate rolling a die.
rolls = []
for x in range(10):
    roll = randint(1,6)
    rolls.append(roll)

    # Examine the length and size of the list.
    list_length = len(rolls)
    list_size = sys.getsizeof(rolls)
    print(f"Items: {list_length}\tBytes: {list_size}")

After appending each item, we print out the number of items, and the size of the list in bytes. Here’s the output:

Items: 1    Bytes: 88
Items: 2    Bytes: 88
Items: 3    Bytes: 88
Items: 4    Bytes: 88
Items: 5    Bytes: 120
Items: 6    Bytes: 120
Items: 7    Bytes: 120
Items: 8    Bytes: 120
Items: 9    Bytes: 184
Items: 10   Bytes: 184

This list takes up 88 bytes of memory when it has one item in it. But, remember that Python didn’t just grab enough room for one item; it assumes we’re going to keep adding items, so it grabbed enough space to hold a number of items. That initial space was enough to store the first four items. When it’s time to add a 5th element, Python grabs some more space — 120 bytes overall. This is enough for the next four elements.

It’s pretty interesting to visualize this. Here’s a bit of Matplotlib code to visualize the size of the list over the first 100 items:

# list_memory_visual.py

import sys
from random import randint

import matplotlib.pyplot as plt

# Build a list of random numbers, to simulate rolling a die.
rolls = []
sizes = []
for x in range(100):
    roll = randint(1,6)
    rolls.append(roll)

    # Record the size of the list on each pass through the loop.
    list_size = sys.getsizeof(rolls)
    sizes.append(list_size)

# Plot the size of the list vs the number of items.
plt.style.use("seaborn")
fig, ax = plt.subplots()

x_values = list(range(1, 101))
ax.plot(x_values, sizes)

ax.set_title("Size of list vs number of items in list", fontsize=24)
ax.set_xlabel("Number of items", fontsize=14)
ax.set_ylabel("Size of list (bytes)", fontsize=14)

plt.show()

We make a new list called sizes, to keep track of the size of the list on each pass through the loop. Then we plot the size of the list against the number of items in the list. The result is pretty cool if you haven’t seen this visualization before:

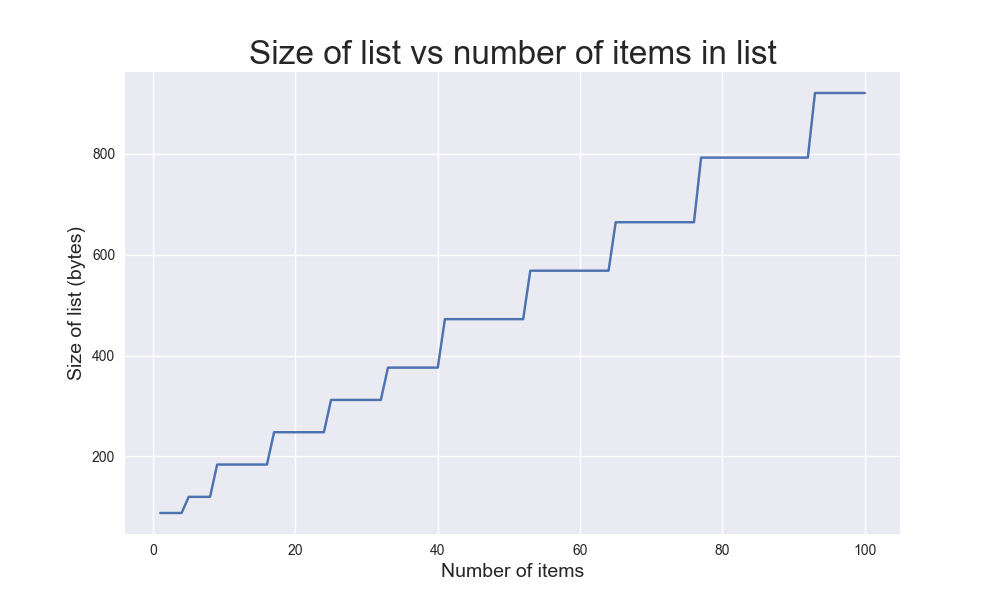
Here you can actually see how Python grabs chunks of memory at a time. When the list is small, it grabs smaller chunks. As the list grows, it grabs larger and larger chunks of memory. If you generate this same plot for a list with a million, or ten million items, you’ll see similar patterns in every plot.

Note: The size of a list doesn’t depend on the size of the elements in the list. In memory, a list is really a sequence of references to where the actual objects are stored in memory. Two lists that have the same number of items will have roughly the same size in memory, regardless of how big or small the items in each list are.

Conclusions

The biggest takeaways here aren’t that you should use a deque in some situations, or that you should know how much memory Python grabs as a list expands. Those are interesting details, but the big idea is to understand that Python is managing memory so that, most of the time, you don’t have to. When your programs involving lists do slow down, a decent understanding of how Python manages lists can help you come up with an approach that should be more efficient.

In the next post in this series, we’ll look at some other data structures that are more efficient than lists in specific situations. These structures will build on the ideas we’ve dealt with here; we’ll see a variety of ways that Python keeps a balance between simplicity and efficiency.

Resources

You can find the code files from this post in the mostly_python GitHub repository.

Further exploration

If you’re curious and looking to write some code, there are a number of ways you can explore the ideas brought up in this post.

Note: If you’ve done formal profiling or benchmarking before, feel free to take a more structured approach to these exercises.

1. Finding the limits of your system: append()

On my system I can build a simple list of about 20 million items, in just over 10 seconds, using append(). How large of a list can you make on your system, without any optimization? Try this using the random_numbers.py example shown above, or write your own program to find these limits.

2. Finding the limits of your system: insert()

Build the same list using insert(0, item) instead of append(). How many items does your list contain after the program runs for about 10 seconds?

3. Using a deque

Rewrite your previous program using a deque instead of a list. How much faster does the program run, to make a sequence of the same length? How long of a sequence does your program generate if you let it run for about 10 seconds?

4. Visualizing memory usage

The only plot in this discussion shows the memory footprint of a list as it grows to contain 100 items. Recreate this plot on your system, either using the code you see here or a plotting library you prefer working with. Generate a series of plots for sequences of various lengths. Which aspects of the plot are consistent regardless of the number of items? Which aspects change as the number of items changes?

5. Memory and list contents

Make two lists, each having the same number of elements. One list should be very simple; every element should be a small integer, or a single character. The other list should contain very large items. For example, your list might contain really long strings, like this:

long_strings = ["a"*10_000, "b"*10_000, "c"*10_000]

Call getsizeof() on each of your lists, and see how the size of the list containing small items compares to the size of the list containing much larger items.

Note: It may be helpful to call getsizeof() on some of the individual items in your list. You should be able to make a list whose overall size is smaller than some of the individual items in the list.

6. Thinking about data

If any of this is new to you, what does it clarify for you about Python, and about programming in general? What questions does it raise?