Birthdays and lotteries
MP 120: I rarely play the lottery, but when I do I like to model it afterwards.
I've written recently about surviving a pretty serious medical event and then making it through a hurricane with some life interruptions, but no significant harm. When I was in the hospital, I told myself that I'd been lucky in enough ways that I should buy a lottery ticket when I got out.
I don't buy lottery tickets very often, so when I do I like to go all in. I bought a ticket for the North Carolina Powerball Lottery, which currently has a top prize of around $400m. That's life changing money! I've bought about three lottery tickets in my life, so I don't have any established approach to picking numbers. My family got me through these recent hard times, so I chose numbers that came from our birthdays. Later, I started wondering if limiting my choices to the values 1-31 would affect our chances of winning, since you can pick numbers from 1 through 69.
In this post I'll walk through a quick, simple check of that question. It feels like only choosing numbers between 1 and 31 should roughly cut our chances of winning in half. But when I think more rationally it seems like any set of numbers should have the same chance of winning as any other.
Lotteries make me feel uncomfortable
I've only gambled a handful of times in my life, and I really dislike state-sponsored gambling. I've stood in convenience store checkout lines many times, watching people mindlessly scratching off small-stakes lotto tickets. It's pretty sad to see people make a small pile of "winning" tickets, only to trade that pile in for a smaller batch of new tickets. It's pretty clearly addictive, yet we still fund so many programs with lottery proceeds.
When I decided to buy a ticket, I had to read a bunch before I could figure out how to play. It's interesting to see all the warnings about how this can become an addiction. This post is not an endorsement of gambling; if everyone went through the process of modeling lotteries I think they'd be a bit less popular.
Modeling the lottery
The NC Powerball lottery has a number of ways you can win. A lot of it is tied to the "Powerball", a specific ball that increases most of the prizes if you guess it correctly. To keep this simple, I'll ignore the Powerball and just focus on the core aspect of the lottery: trying to match 5 numbers between 1 and 69.
Let's write a function to get a ticket:
from random import randint def get_ticket(ticket_size=5, max_value=69): """Get a ticket of ticket_size numbers. Numbers are picked from 1 through max_value). """ ticket = [] while len(ticket) < ticket_size: pulled_number = randint(1, max_value) # Don't reuse numbers. if pulled_number in ticket: continue ticket.append(pulled_number) ticket.sort() return ticket breakpoint()
The randint() function returns a random integer between the two values provided. It's important to note that this function can return the starting and ending numbers, as well as every number in between.
The function get_ticket() takes two arguments. The ticket_size argument specifies how many numbers should be generated for a specific ticket. The max_value argument specifies the largest number you can choose for the given lottery. The default values here match the rules for the NC Powerball lottery. Lottery tickets typically show numbers in ascending order, rather than the order that numbers are pulled, so the list representing the ticket is sorted before being returned.
When doing exploratory work like this, I like to put a breakpoint at the end of the file, and play around with the code before moving on. Let's run this program, and make a few tickets in the debugging session:
$ python nc_powerball.py -> breakpoint() (Pdb) quick_pick = get_ticket() (Pdb) quick_pick [19, 20, 21, 55, 69] (Pdb) birthday_ticket = get_ticket(5, 31) (Pdb) birthday_ticket [7, 9, 14, 23, 24] (Pdb) winning_draw = get_ticket() (Pdb) winning_draw [9, 13, 20, 31, 40]
Here I'm using get_ticket() in three ways. First, the lottery lets you choose a "Quick Pick" ticket, where the machine generates a random ticket for you. This can be simulated by calling get_ticket() with no arguments.
For birthday_ticket I'm limiting the numbers to 1-31, which generates a ticket someone might play if they use people's birthdays to pick numbers. To get a set of winning numbers, assigned to winning_draw, the default arguments again suffice.
Checking tickets
We need to be able to check if a ticket is a winner. Here's a function that accepts a ticket, and compares it against the winning numbers that were drawn:
def check_ticket(ticket, winning_draw): """Find out how many numbers matched.""" matches = 0 for num in ticket: if num in winning_draw: matches += 1 return matches
I like to start with the simplest solution to a problem, especially when writing about code. The function check_ticket() first sets the number of matches to zero. It then looks at each num in the ticket that was played, and looks to see if that number is in the winning draw. If it is, it increments the number of matches for this ticket. After it runs through all the numbers in the ticket, it returns the number of matches.
If you're new to Python, that's a perfectly reasonable way of checking a ticket. However, we can write a much shorter function using a comprehension:
def check_ticket(ticket, winning_draw): """Find out how many numbers matched.""" matches = [num for num in ticket if num in winning_draw] return len(matches)
This version of check_ticket() generates a list called matches. That list is built by looping over the numbers in the played ticket (num for num in ticket), but only keeping the values that are in the winning draw (if num in winning_draw). We then return the length of matches.
We can even make this a one-line function:
def check_ticket(ticket, winning_draw): """Find out how many numbers matched.""" return len( [num for num in ticket if num in winning_draw])
Now that we have a way of checking played tickets against winning draws, we can simulate a drawing.
Simulating my chances
Let's make multiple drawings, and see how often a given birthday ticket would win. There are multiple ways to win, so I'll show how many times one number matched, how many times two numbers matched, and so forth.
The NC lottery lets you play a ticket in just one drawing, or keep playing the same number for up to 30 drawings. I was only buying one ticket, so I chose to play it for the full 30 drawings, just to extend the fun for a while. To model this, we'll generate one ticket, and then check that same ticket against a series of drawings.
Here's a simulation of playing a single "birthday ticket" in 30 consecutive drawings:
from random import randint def get_ticket(ticket_size=5, max_value=69): ... def check_ticket(ticket, winning_draw): ... bd_ticket = get_ticket(5, 31) print(f"Birthday ticket: {bd_ticket}\n") # Simulate a number of drawings. results = {0:0, 1:0, 2:0, 3:0, 4:0, 5:0} for _ in range(30): winning_draw = get_ticket() matches = check_ticket(bd_ticket, winning_draw) results[matches] += 1 # Show results. for num, num_matches in results.items(): print(f"Match {num}: {num_matches}")
We first generate a "birthday ticket", assigned to bd_ticket. We then set up an empty dictionary called results. The keys represent the number of matches, and the values are the number of tickets with that many matches. For example, if you want to know how many tickets matched three numbers from the winning draw, you'd use the code results[3].
We then make a loop that runs 30 times. On each pass through the loop we draw a set of winning numbers, assigned to winning_draw. We get the number of matches for that drawing by calling check_ticket(), using the same ticket (bd_ticket) for each drawing. If there are no matches, we increment results[0]. If there's one match, we increment results[1]. This is represented generally by incrementing results[matches].
Finally, we show the results by looping over the results dictionary, printing the number of matches for each key in the dictionary. Here's a sample run:
$ python nc_powerball.py Birthday ticket: [3, 6, 12, 16, 24] Match 0: 25 Match 1: 5 Match 2: 0 Match 3: 0 Match 4: 0 Match 5: 0
In this example, which was typical over multiple runs, there were 25 drawings where bd_ticket matched no numbers at all. There were 5 drawings where one of the numbers from bd_ticket matched.
In the actual NC Powerball lottery, it's likely that none of these 5 tickets would have won anything at all. You get a small prize ($4) for matching one number, but only if you also match the Powerball. The Powerball can be any number from 1 through 36. I'm not going to model the Powerball, but it would reduce the number of winners at the "Match 1" level by a factor of 36.
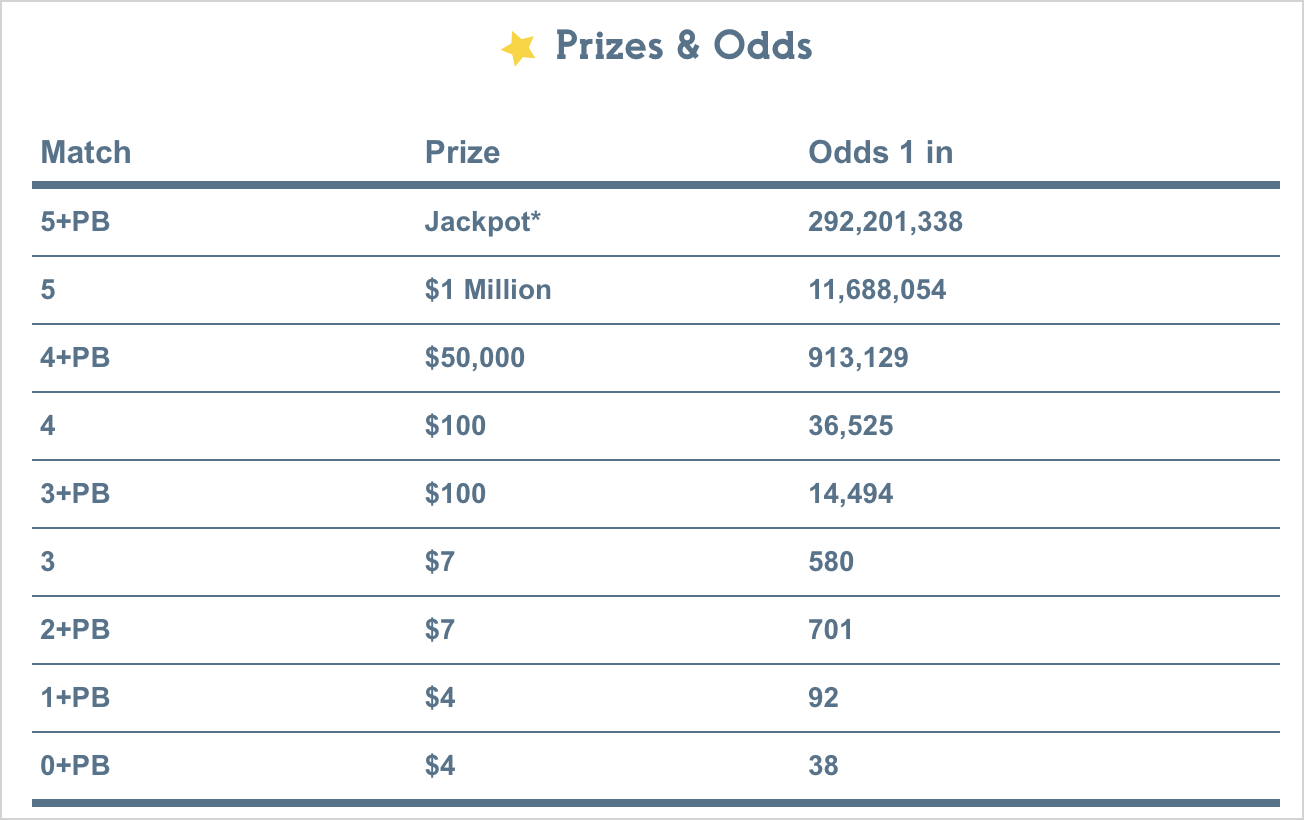
You get something for matching 3 and 4 numbers without matching the Powerball, but not much. For example you'd win $100 for matching 4 numbers without the Powerball, but you'd get $50,000 for matching 4 numbers and the Powerball.
The only significant outcome without matching the Powerball is for matching 5 numbers. If you match 5 without the Powerball, you get $1 million. Matching 5 with the Powerball wins the jackpot, which is currently almost $500 million.
Birthday tickets vs Quick Pick tickets
Now let's go back to the original question that inspired this whole post:
Does playing a "birthday ticket" reduce your chances of winning when there are more than 31 choices for each number in the ticket?
Let's find out by making the same birthday ticket we've been making, but also make a Quick Pick ticket. We'll then print the results for both tickets, and see if there's a significant difference:
... bd_ticket = get_ticket(5, 31) quick_pick = get_ticket() print(f"Birthday ticket: {bd_ticket}") print(f"Quick Pick: {quick_pick}") # Simulate a number of drawings. bd_results = {0:0, 1:0, 2:0, 3:0, 4:0, 5:0} qp_results = {0:0, 1:0, 2:0, 3:0, 4:0, 5:0} for _ in range(30): winning_draw = get_ticket() matches = check_ticket(bd_ticket, winning_draw) bd_results[matches] += 1 matches = check_ticket(quick_pick, winning_draw) qp_results[matches] += 1 # Show results. print("\n\t\tBirthday\tQuick Pick") for num in bd_results.keys(): print(f"Match {num}:\t{bd_results[num]}\t\t{qp_results[num]}")
The logic here hasn't changed significantly from the previous listing. We make two tickets instead of one. We make two dictionaries for results as well, bd_results and qp_results. In the loop, we check the number of matches for each ticket, for every drawing in the loop. When it's time to show the results, we create a table showing how many matches each ticket has.
Here's the output for the first run:
$ python nc_powerball.py Birthday ticket: [3, 10, 17, 20, 22] Quick Pick: [16, 27, 38, 55, 60] Birthday Quick Pick Match 0: 21 20 Match 1: 7 10 Match 2: 2 0 Match 3: 0 0 Match 4: 0 0 Match 5: 0 0
With only 30 draws, there doesn't seem to be a whole lot of difference between the two tickets. If we took into account the Powerball, it's likely that none of these tickets would have won anything at all.
Simulating many drawings
Now let's increase the number of drawings, and see if the pattern holds for larger runs. I'm going to increase the number of drawings until the program starts to slow down on my system.
At about one million drawings, the program takes just over 2 seconds to run on my M2 MacBook Air:
$ time python nc_powerball.py Birthday ticket: [15, 16, 25, 27, 30] Quick Pick: [25, 31, 42, 46, 54] Results for 1,000,000 drawings: Birthday Quick Pick Match 0: 678,602 678,211 Match 1: 282,430 282,665 Match 2: 37,188 37,288 Match 3: 1,744 1,808 Match 4: 36 28 Match 5: 0 0 python nc_powerball.py 2.32s user 0.02s system 96% cpu 2.420 total
I modified the code slightly to show the number of drawings, and format the results better. These results are enough to convince me that limiting your choices to numbers that appear in birthdays doesn't actually affect the chances of winning. If there was a difference, I'd expect it to show up in a simulation with this many drawings. In particular, I'd expect to see a significant difference in the number of tickets matching 1 through 4 numbers.
What about the ticket [1, 2, 3, 4, 5]?
I like how modeling real-world situations often lets you explore new questions that come up as you're working. One of the things I started wondering about involved taking this idea of reducing the numbers you choose from to the extreme: What if you only played the numbers 1, 2, 3, 4, 5? I expect many people would think "That ticket would never win, the lottery would never come up with those five numbers!" But thinking about it rationally for a moment, those numbers seem just as likely to win as any other set of five specific numbers.
We can answer this question by changing one line of code:
bd_ticket = [1, 2, 3, 4, 5]
Instead of calling get_ticket() to get a random ticket based on birthdays, we assign the list [1, 2, 3, 4, 5] to bd_ticket. Here's an example set of results with this one change:
$ python nc_powerball.py Birthday ticket: [1, 2, 3, 4, 5] Quick Pick: [19, 30, 36, 39, 46] Results for 1,000,000 drawings: Birthday Quick pick Match 0: 675,142 674,013 Match 1: 285,231 285,721 Match 2: 37,716 38,376 Match 3: 1,887 1,852 Match 4: 24 38 Match 5: 0 0
It turns out the ticket [1, 2, 3, 4, 5] doesn't perform any worse than any other ticket over a million drawings. It doesn't necessarily make intuitive sense right away, but it makes sense mathematically.
Conclusions
I'm not a fan of gambling, but it seems to be part of human nature in some ways. A little familiarity with programming concepts lets you model many lotteries and gambling-related games, which can give you an empirical sense of how things work. People's intuitions about random events aren't always accurate, which is part of why lotteries and casinos make so much money. Checking your intuitions by modeling games of chance can be a great way to find out whether your intuition about a particular game is accurate or not.
This was quick exploratory code. If you find this investigation interesting, there are many ways it could be refactored and optimized. For example get_ticket() can be reduced to one line of code using the sample() function from the random module. I don't think that approach makes the code more efficient, but it does make it shorter. I'm sure using sets, tuples, and arrays instead of lists would start to improve the performance of the code. If you're interested in improving this code, make sure you do some profiling so you're focusing on the sections of code that are actual bottlenecks.
One last note, naming things really is hard sometimes! I was using the name my_ticket for a while, before coming up with the more specific name birthday_ticket (and the shorter bd_ticket). Also, I was using winning_ticket for a while, but kept feeling like there were too many things called "ticket". I realized I was talking about drawings, and started using winning_draw instead. These are small changes, but they affect the way we think about what we're modeling. If you come up with a more specific name for something in your code, don't be afraid to take the time to switch to the better name. That's an especially good habit if you're in the early stages of a project, when it's easier to make those kinds of changes.
Resources
You can find the code from this post in the mostly_python GitHub repository.