Financial literacy with Python

MP 123: Modeling mortgage loans, to help make clearer financial decisions.

We're in the process of buying a house, and whenever we go through this process I spend a lot of time looking at all the different options about taking out such a significant loan. I always do a fair bit of my own analysis, and I always feel for people who aren't able to carry out this kind of analysis. It would not feel good to have to take a loan officer's word about what's possible, and what's best for us in the long run.

I usually use a spreadsheet because it's easier to show the analysis to other people. But I've also written short programs to validate what loan officers have shared, and to consider different ways of setting up a loan. We've moved a number of times now, and I've found mistakes in the loan paperwork numerous times over the years. I've also come to conclusions that are much better for us than what the loan officer had suggested. (It's good to keep in mind that the "loan officer" is really a "loan salesperson". Also, many loan officers have a deep understanding of how loans are structured, but many do not and are just punching numbers into a web app and trusting what they see.)

If you know some basic Python, you can start to do your own loan analysis. You don't have to model every aspect of a real-world loan to get some benefit from this. Even modeling a few factors can help you make sense of the actual numbers, even if they vary somewhat from your model. If you've never done this kind of analysis before, you'll almost certainly come away with a better understanding of how complex loans work. You'll end up in a better position to make important decisions about your finances.

Shopping for loans in 2024

I'll share a quick observation about something I've noticed from shopping for a mortgage loan this time around. In all our previous purchases, when I compared loans from different banks, they all advertised their base rates. You could then ask about points. Points can seem complicated if you don't already understand how payments are calculated for a loan. Basically, it's a system where you pay a lump sum up front in order to get a lower interest rate for the life of the loan. For the life of the loan is the key phrase there; if you're going to hold the loan for a long time, it might be worthwhile to pay more up front in order to lower your interest rate. But if you sell your house after just a few years, it can end up being more expensive than just accepting the base rate.

When comparing loans for the home we're in the process of buying, I've noticed that most banks seem to be advertising rates that assume you're going to use points to get a reasonable rate. That makes it much harder to compare loans without doing some analysis; you have to read the fine print and figure out how much they're going to charge you for that rate. My best guess is they're doing this because rates have gone up so much. When rates were around 3% they didn't seem to mind posting their base rate, and you could then ask about using points. Now they don't want to advertise a base rate of 7.5%, when their competitors are advertising a points-assumed rate of 7.125%.

If you're shopping for a loan, be aware of this tactic.

Analyzing a mortgage loan from first principles

One nice thing about using Python to analyze a mortgage loan is that you can build an intuitive understanding of how loans work in general, and how mortgage loans work in particular. This happens naturally when you make some simple assumptions about paying off a loan, and then start adding in more details. Every time I've done this, it's made me reconsider looking for a career in finance. I don't love money, but clarity around financial decisions is a wonderful thing.

Simplest model of a loan

There are formulas for calculating the monthly payment for a loan. But if you don't know where that formula comes from, it ends up being a black box that spits out a number you just have to trust. Instead of using a formula, let's figure out how to pay off a loan more intuitively.

The simplest model of a loan requires three pieces of information:

"""Analyze a mortgage loan."""

purchase_price = 500_000
interest_rate = 0.075
loan_term = 360

You need to know how much you're taking the loan out for, what the interest rate is, and how many payments you'll have to make. Everything else can come later: down payment, PMI, taxes, points, etc.

As an example I'm using a purchase price of $500,000, an interest rate of 7.5%, and a standard loan term of 30 years. A 30-year mortgage typically consists of 360 monthly payments. (Note that this is an interest rate of 7.5%, not an APR of 7.5%.)

Calculating the monthly payment

Now we can ask the key question:

How much will I need to pay each month to pay off the loan in its entirety?

We'll let the computer figure this out by setting a really low monthly payment, and increasing it steadily until it's enough to pay off the loan:

...
# Find a monthly payment that pays off the loan.
monthly_payment = 1.00
principal = purchase_price

I set the monthly payment to $1.00. This would never work for a home loan, and that's the point. We start with a value we know is far too low, and keep increasing it until it's enough to pay off the loan. We also set the principal to the purchase price of the house. If you're not clear on the term, principal refers to how much is still owed on the loan at any point in the loan's life.

Now we'll set up a loop to see if this amount is enough to pay off the loan:

...
while True:
    # Run the life of the loan with the current payment.
    for payment_num in range(loan_term):
        interest = (interest_rate/12) * principal
        toward_principal = monthly_payment - interest
        principal -= toward_principal

    # Summarize results.
    print(f"Tried {monthly_payment:,.2f}")
    print(f"  Remaining principal: {principal:,.2f}")

    # Exit loop if loan is paid off.
    if principal <= 0:
        break

    # Loan was not paid off. Increase monthly payment, and reset loan.
    monthly_payment += 1.00
    principal = purchase_price

The outer while loop is infinite; we'll break out of it when we've found the right monthly payment. Inside the loop, we simulate the entire life of the loan, for the current value of monthly_payment. Each iteration of the for loop corresponds to one month in the life of the loan. For each month, we calculate the following:

• This month's interest. This is the annual interest rate divided by 12, times the remaining principal.
• How much of this month's payment is going toward_principal. This is the amount you pay each month, minus that month's interest. (This is a depressingly small number at the start of a loan!)
• The updated principal. In this simplified model, the amount that doesn't go towards interest goes to paying off the principal. In more detailed models, you'd account for costs like PMI here as well.

After the loop runs for 360 months, we print a summary showing the monthly payment that was just used, and how much of the principal was left over. Then we see if the principal has been paid off in full. If it has, we break out of the while loop.

Finally, if we're still in the while loop, we increase the monthly payment and reset the principal to the purchase price.

Here's the results:

$ python mortgage_calculator.py
Monthly payment: 1.00
  Remaining principal: 4,709,419.51
Monthly payment: 2.00
  Remaining principal: 4,708,072.06
...
Monthly payment: 3,495.00
  Remaining principal: 1,445.19
Monthly payment: 3,496.00
  Remaining principal: 97.75
Monthly payment: 3,497.00
  Remaining principal: -1,249.70

If you pay $1.00 a month towards a mortgage, you end up accruing unpaid interest every month. You're paying way less than the monthly interest, so the principal just keeps increasing. After 30 years, you'd owe almost $5,000,000! It takes a monthly payment of about $3,497.00 to pay off the loan in 30 years. You can set the increment to $0.01 if you want a precise monthly payment.

It's rare that the remaining principal after the 360th month is exactly zero. In an actual loan, you end up making 359 full payments and one final smaller payment to finish paying off the loan.

Summarizing costs

Now that we have a reliable way of calculating the monthly payment, we can summarize the actual loan:

"""Analyze a mortgage loan."""
...

total_principal = 0
total_interest = 0
while True:
    # Run the life of the loan with the current payment.
    for payment_num in range(loan_term):
        interest = (interest_rate/12) * principal
        toward_principal = monthly_payment - interest
        principal -= toward_principal

        total_interest += interest
        total_principal += toward_principal

    # Exit loop if loan is paid off.
    if principal <= 0:
        break

    # Loan was not paid off.
    # Increase monthly payment, and reset loan.
    monthly_payment += 1.00
    principal = purchase_price
    total_principal = 0
    total_interest = 0

# Summarize loan.
total_paid = total_principal + total_interest
print("Loan summary:")
print(f"  Purchase price: ${purchase_price:,.2f}")
print(f"  Monthly payment: ${monthly_payment:,.2f}")
print(f"  Principal paid: ${total_principal:,.2f}")
print(f"  Total interest paid: ${total_interest:,.2f}")
print(f"  Total paid: ${total_paid:,.2f}")

We track the total amount that goes toward the principal, and the total that goes toward interest. I also removed the lines that report all the failed attempts at guessing a correct monthly payment.

After the loop has finished, we summarize all these values:

$ python mortgage_analysis.py
Loan summary:
  Purchase price: $500,000.00
  Monthly payment: $3,497.00
  Principal paid: $501,249.70
  Total interest paid: $757,670.30
  Total paid: $1,258,920.00

The principal paid should match the purchase price, within the margin of one monthly payment. (With all real-world factors included in the model, such as an exact monthly payment and an adjusted final payment, they would match exactly.)

With the numbers used in this example, you'd pay just over $750,000 in interest over the life of the loan. The true cost of this home would be just over $1.25 million.

Comparing to mortgage calculators

There are many online mortgage calculators that help people get these numbers if you can't do the analysis yourself. For example, here's what mortgagecalculator.org gives for the parameters used so far:

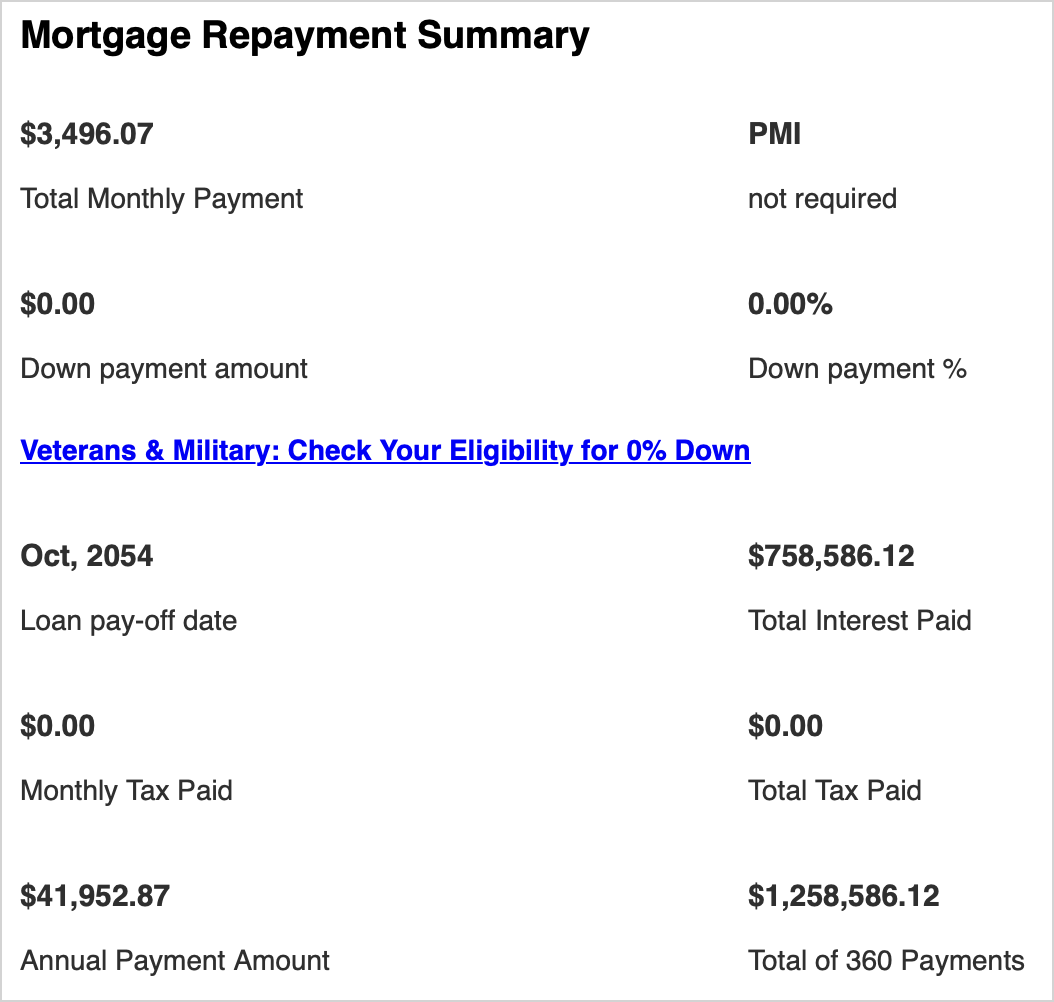
All of these numbers roughly match what we've calculated.

Adding more details

If you've never analyzed a loan before and this is as far as you go, this should give you a lot more confidence in reviewing the numbers on an actual mortgage. But if you find this helpful or interesting, you can start to add more details to make the calculations more realistic and useful.

Let's add a down payment to the model:

"""Analyze a mortgage loan."""

purchase_price = 500_000
interest_rate = 0.075
loan_term = 360
down_payment = 15_000
loan_amount = purchase_price - down_payment

# Find a monthly payment that pays off the loan.
monthly_payment = 1.00
principal = loan_amount

total_principal = 0
total_interest = 0
while True:
    ...
    # Loan was not paid off.
    # Increase monthly payment, and reset loan.
    monthly_payment += 1.00
    principal = loan_amount
    total_principal = 0
    total_interest = 0


# Summarize loan.
total_paid = down_payment + total_principal + total_interest
print("Loan summary:")
print(f"  Purchase price: ${purchase_price:,.2f}")
print(f"  Down payment: ${down_payment:,.2f}")
print(f"  Loan amount: ${loan_amount:,.2f}")
print(f"  Monthly payment: ${monthly_payment:,.2f}")
print(f"\n  Principal paid: ${total_principal:,.2f}")
print(f"  Total interest paid: ${total_interest:,.2f}")
print(f"  Total paid: ${total_paid:,.2f}")

We include a line for the down payment, which I've set to 3% of the purchase price for this example. We add a new variable called loan_amount, which is how much you borrow to purchase the house. This is the starting value for the principal, and it's what we reset the principal to on each pass through the loop that calculates the monthly payment.

The value for total_paid includes the down payment, and we include the down payment in the final summary. The summary is getting longer, so we also break it into two parts:

$ python mortgage_analysis.py
Loan summary:
  Purchase price: $500,000.00
  Down payment: $15,000.00
  Loan amount: $485,000.00
  Monthly payment: $3,392.00

  Principal paid: $486,090.94
  Total interest paid: $735,029.06
  Total paid: $1,236,120.00

The monthly payment has dropped by about $100. The total paid over the life of the loan, however, has dropped by just over $20,000.

What else can you do?

So far, everything shown here can be found by running your numbers on a simple online mortgage calculator. But once you have this set up, you can answer all kinds of questions that are difficult or impossible to answer with an online calculator:

• I live in Alaska. What happens if I put my PFD towards the mortgage every year?
• What happens if I make one extra payment each year? (Usually this is done by doubling one payment each year.)
• What happens if I increase the amount I pay each month by $50 every year?
• Can I print a matrix of different down payments and interest rates, to help choose from all the options?
• What would a 15-year loan look like?
• The loan officer keeps talking about points. How long would I have to keep this loan for points to be worthwhile?
• What does a graph of the amount paid vs the remaining balance look like over time?

Most of these questions can be modeled with a bit of trial and error, even if you don't fully understand how to approach them right away. Trying to model them pushes you to ask specific questions that build your understanding of how all of this works. You can also write a loop that prints out a summary of the state of the loan after each of the 360 payments. If you're modeling something like an extra payment each year, you should be able to see the impact that extra payment makes by scrolling through the output and examining the state of the loan around those double payments. If your code is off, this can help see where the calculations are going wrong.

If the numbers you come up with don't match what your loan officer is telling you, figure out if there's a mistake in your work, or theirs. Maybe you forgot to include a factor such as PMI? Maybe they used the wrong percentage somewhere? I've found small but meaningful errors in about half the loans we've taken out in the last couple decades, and I've found plenty of mistakes in my own work as well.

Conclusions

Simple, short term loans can be quite easy to model. More complex, long term loans can be harder to model. Mortgages tend to be long term, and more complex than most loans people deal with. The more you understand them, the more confidence you'll have making decisions about your loan. You'll also be less likely to accept things that sound good, but end up more advantageous to the bank than to you. And you'll be less likely to fall for predatory loans as well.

In the US, we're heading into a period of deregulation. One of the things most of us can agree on is that we're almost certainly going to see an increase in scams, and an increase in deceptive business practices. That makes it all the more important to be able to figure out what should be happening when taking out a loan, and make sure that the loan you end up signing for meets those conditions. If you're not in the US your mortgages are probably structured somewhat differently, but the main principles should apply across many regions.

Resources

You can find the code from this post in the mostly_python GitHub repository.